�P�D�ړI
�����v��p���ăv���Y���̒��p�ƍŏ��̂ӂ�Ƃ𑪒肵�A�v���Y���̋��ܗ����Z�o���邱�ƁB
�Q�D���_
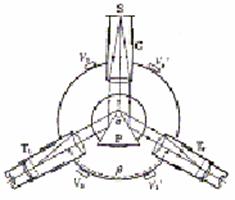
�}1�̂悤�ɁA�v���Y���`�a�b�߂���P�F��LMM�fT�ł���Ƃ��A���ꂪAB�CAC���ʂ̖@��ƂȂ��p���A���ꂼ��i,r,i',r'�Ƃ��A���̏ꍇ�̂ӂ�����Ƃ���A
����(i�|r)�{(i'�|r')��(i�{i')�|(r�{r')
�Ƃ���ŁA�v���Y���̒��p�����Ƃ���A
r�{r'����
���@��i�{i'�|��
�܂��A�v���Y���̋��ܗ���n�Ƃ���A
sin i �^sin r ��sin i' �^sin r�f��n
�]���āA
i =sin-1 ( n sin r )
i' =sin-1�on sin (���|r )�p
���������āA��sin-1 ( n sin r )�{sin-1�on sin (���|r )�p�|���ŏ��l�����߂�ɂ́A
�䂦�ɁA�̍ŏ��l�����߂�ɂ́A
���^������ n cos r�^��(�P�|n2 sin2 r)�|n cos(���[��)�^��(�P�|n2sin2(���[��))
�����O�����[���O�@�@�@�@�����O�����^�Q
�����O�����O�������^�Q
���������čŏ��l�̂ӂ�����O�Ƃ���A
i0��i0�����i���{���O�j�^�Q
���Ȃ킿�A�������v���Y����Ώ̓I�ɒʉ߂��鎞���ŏ��̂ӂ�ł���A�v���Y���̋��ܗ��́A
n��sin i�O �^sin r�O��sin{�i���{���O�j�^�Q}�^sin (���^�Q)
���������āA�v���Y���̒��p���ƒP�F���ɑ���ŏ��̂ӂ���O�Ƃ𑪒肷��A���̔g���ɑ���v���Y���̋��ܗ�n���Z�o�ł���B
�R�D���u
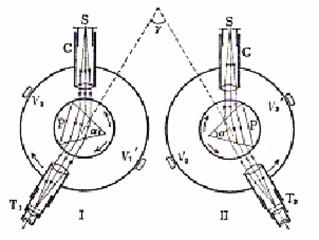
�@�@�@������ENa�����ȂǁB�����v�͑�P�}�̂悤�ȑ��u�ŁAC��collimator�AP��prism�AT��telescope�AD��dial�AV��vernier�ł���B�܂��A��Q�}�́A�����pNa���d�ǂ��P�O�OV�̌𗬓d������g�p���鑕�u�������B
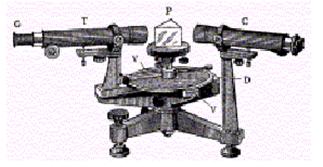
��P�}

��Q�}
�S�D�������@
�@�@�@�����v�𐳂����g�p���ăv���Y���̋��ܗ��𑪒肷��ɂ́A���̒��������Ă���A�v���Y���̒��p�ƍŏ��ӂ�𑪒肵�Ȃ���Ȃ�Ȃ��B
(1)�]�����s�����ɍ��킷
�����v����]�������͂����Ē��ׂ�ƁA���̓��͑�R�}�̎����悤�ɂR�{���琬��B�܂��b�������ď\�F�����͂����茩����悤���߂��A�a�C�b�݂͌��ɌŒ肵�Ȃ���`�������ĉ����̕��́i�d���Ȃǁj���悭�����āA�������\�����Ƃ̊ԂɎ����̂Ȃ��悤�ɒ��߂���B���Ȃ킿�A�ڂ������������Ă��A���̂̑��Ə\�����Ƃ̊Ԃɑ��ΓI�ψʂ��Ȃ���悢�B�������āA�]�������������A���Ȃ킿���s�����ɍ������̂��́A���̂܂ܕ�����Ɏ��t���AA�AB�AC�̓��̑��ΓI�ʒu�́A���������������ĕω����Ă͂Ȃ�Ȃ��B
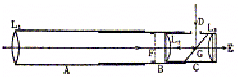
��R�}
|
��S�} |
(�Q)�v���Y���̒��p�̑���
��S�}�̂悤�ɑ��낤�Ƃ���v���Y��P�̒��p����collimator C�Ɍ����ăZ�b�g���AC����̕��s����������ɓ��Ă�Ƃ��A�v���Y���̍��ʂ�蔽�˂��������ڂ����傤�s�P�Ŋώ@���A�X���b�g�r�̑����\�����ƍ��킹���Ƃ��̂s�P�ɌŒ肵��vernier�̈ʒu���_�C�����œǂ�łu�P�C�u�P���Ƃ���B���ɖ]�������s�Q�̈ʒu�܂ʼn�]���āA�o�̉E�ʂ���̔��ˌ��ɂs�Q�����킹���Ƃ���vernier�̓ǂ݂��u�Q�C�u�Q���Ƃ���A�]������]�p�A���Ȃ킿���ˌ����̃v���Y���̒��p���̗��ʂɂ�锽�ˌ��̊J�����́A�u�Q�[�u�P�A�u�Q���|�u�P���̕��ςƂȂ�B�Ƃ��낪�A���ʊw����A
�������^�Q
|
��T�} |
�@�ł��邱�Ƃ��ȒP�ɏؖ��ł��邩��A�]�����̉�]�p���𑪒肷��A���̔������v���Y���̒��p���ł���B
(�R)�ŏ��ӂ�p�𑪒�
�܂���T�}�T�̂悤��collimator �b�A�v���Y�� �o, telescope �s�P���Z�b�g���A�X���b�g�r�̑����\�����ɑ��Ĉȉ��ɉ^�����邩���ώ@����B�����A���s�����v���Y���̒��_���ɂ��đΏƓI�Ƀv���Y����ʉ߂���ꍇ�A���Ȃ킿�A�ŏ��ӂ���O�ƂȂ��Ă���ꍇ�ɂ́A�o������E������ɉ�]���Ă��A�ӂ�͕K���������邩��A�r�̑��͏\��������ɍ����ɓ����B���Ȃ킿�A�r�̑��̈ړ��̉E�̋Ɍ��ɏ\���������킹�邱�Ƃɂ��A�s�P�̕����̓�0��^����B�����ŁA�s�P�ɌŒ肵��vernier V�P�AV�P�f�̈ʒu��ǂ݂Ƃ�B
���ɁA�b�̈ʒu�͂��̂܂܂Ƃ��A��ܐ}�U�Ɏ����悤�ɁAP�AT�Q�̈ʒu����]����A�O�Ɠ��l�A�o������E�ɉ�]���鎞�s�Q�̍��̋Ɍ��̈ʒu�ɑ���vernier�̈ʒuV�Q�AV�Q�f��ǂݎ�邱�Ƃ��ł���B�������āAV�Q�[V�P�AV�Q���|V�P�f�̕��ϒl�����Ƃ�A�ŏ��̂ӂ�́A
��0 =���^�Q
�ɂ��^������B
(�S)�v���Y���̋��ܗ��̎Z�o
���āA�v���Y���̒��p���ƁA���̔g���i�m���̂c���Ȃ���c = 5893���j�ɑ��邻�̃v���Y���̍ŏ��̂ӂ��0�Ƃ𑪒肷��A�v���Y���̋��ܗ��́A
����sin{(���{��0)�^�Q}�^sin(���^�Q)
�ɂ��Z�o�ł���B
�T�D��������
�@�@(�P) �v���Y���̒��p�̑���
|
�s�P�̈ʒu |
�s�P�̈ʒu |
vernier�̈ړ� |
|
�u�P��66º09' |
�u�Q��186º08' |
V�Q�[V�P��119º59' |
|
�u�P'��246º27' |
�u�Q'��6º20' |
V�Q���|V�P�f��-240º07'��119º53' |
�����i119º59'�{119º53'�j�^�Q��119º56'
���@�������^�Q��59º58'
(�Q)�ŏ��̂ӂ�̑���
(i)���F�ɂ���
|
�s�P�̈ʒu |
�s�P�̈ʒu |
vernier�̈ړ� |
|
�u�P��47º21' |
�u�Q��127º35' |
V�P���[V�Q��99º48' |
|
�u�P'��227º23' |
�u�Q'��307º32' |
V�P�|V�Q�f��99º49' |
����(99º48'�{99º49')�^�Q��99º48'30"
���@��0�����^�Q��49º24'15"
(ii)�V�A��(���F)
|
�s�P�̈ʒu |
�s�P�̈ʒu |
vernier�̈ړ� |
|
�u�P��47º15' |
�u�Q��127º52' |
V�P���[V�Q��99º17' |
|
�u�P'��227º23' |
�u�Q'��307º58' |
V�P�|V�Q�f��99º31' |
����(99º17�{99º31')�^�Q��99º24'00"
���@��0�����^�Q��49º42'00"
(iii)�ΐF�ɂ���
|
�s�P�̈ʒu |
�s�P�̈ʒu |
vernier�̈ړ� |
|
�u�P��46º39' |
�u�Q��128º50' |
V�P���[V�Q��98º07' |
|
�u�P'��226º43' |
�u�Q'��308º32' |
V�P�|V�Q�f��97º53' |
����(98º07'�{97º53')�^�Q��98º00'00"
���@��0�����^�Q��49º00'00"
(iv)�Ԃɂ���
|
�s�P�̈ʒu |
�s�P�̈ʒu |
vernier�̈ړ� |
|
�u�P��45º27' |
�u�Q��129º41' |
V�P���[V�Q��95º43' |
|
�u�P'��225º33' |
�u�Q'��309º44' |
V�P�|V�Q�f��95º52' |
����(95º43'�{95º52')�^�Q��95º47'30"
���@��0�����^�Q��47º53'45"
�@�@(�R)�v���Y���̋��ܗ��̎Z�o
�@�@�@�e�F�i���E�V�A���E�E�ԁj�ɂ��āA�X�̃v���Y���̋��ܗ����ȉ��̎���p���ĎZ�o����B
����sin{(���{��0)�^�Q}�^sin(���^�Q)
�@�@�@(i)���F�ɂ���
������sin{(���{��0)�^�Q}�^sin(���^�Q)
�@�@�@�@�@�@�@ ��sin 50º01'53"�^sin 29º59'00"
�@�@�@�@�@�@�@ ��1.63280
�@�@�@(ii)�V�A���ɂ���
���V�A����sin{(���{��0)�^�Q}�^sin(���^�Q)
�@�@�@�@�@�@�@ ��sin 50º08'00"�^sin 29º59'00"
�@�@�@�@�@�@�@ ��1.63276
�@�@�@(iii)�ΐF�ɂ���
������sin{(���{��0)�^�Q}�^sin(���^�Q)
�@�@�@�@�@�@�@ ��sin 50º29'00"�^sin 29º59'00"
�@�@�@�@�@�@�@ ��1.62871
�@�@�@(iv)�ԐF�ɂ���
������sin{(���{��0)�^�Q}�^sin(���^�Q)
�@�@�@�@�@�@�@ ��sin 51º02'08"�^sin 29º59'00"
�@�@�@�@�@�@�@ ��1.61739
�U�D�l�@
�������ʂ��A�v���Y���̊e�F�̋��ܗ��͈ȉ��̂悤�ɂȂ����B
���@�F���� ��1.63280
�V�A���F���V�A����1.63276
�@�F���� ��1.62871
�ԁ@�F���� ��1.61739
�܂��A�J�h�~�E���̊e�F�̌��̔g���͎��̒ʂ�ł���B
�F479.992nm
�F508.582nm
�ԁF6438.47nm
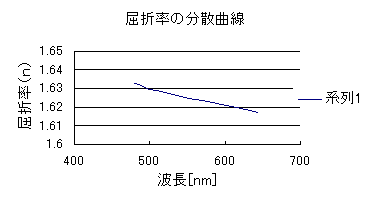
���_��͔g�����Z���Ȃ�ɂ�āA���ܗ��͑傫���Ȃ��Ă����B���ʂƂ��ē���ꂽ���ܗ��U�Ȑ��ɂ���ƁA���_�Ɠ��l�̌��ʂ�����ꂽ�B����āA����̎����͐����ł������ƍl������B�������A�X�����傫���Ȃ��Ă��܂����B����͑�������Ȃ��̂����R�ł���Ǝv���B
|
|
�ۑ�@��P�@�@���𐅕��ɂ��A���̏�ɍڂ���v���Y���������ɂ���B����ɁA�v���Y���Ɏw���ق���Ȃǂ����Ă��Ȃ���Ԃɂ���B
�@�@
�@�@�@��Q�@�@�̗����̔}�����قȂ�ꍇ�͕ψʂƕΊp�̗������������܂��B�ψʗʂ͓����ł����A�Ίp�͎��ɂ���ċ��߂���B�̓K���X�̋��ܗ��ɂ͊W���Ȃ��_�ɒ��ӂ�����������ł���B�Ίp�́A�}��1��3����������1�̋��E�ʂŐڂ��Ă��邩�̂悤�ɔ�������B
�@�@��R�@�@�v���Y���̕Ίp�́A�v���Y���̊p�x���A���ܗ�n �A����ѓ��ˊp�Ƃɂ���Č��܂�B�v���Y�����̌��H���v���Y���p��1/2�̖ʂɐ����ȏꍇ�A�Ίp�͍ŏ��ɂȂ�܂��B�v���Y���p���������ꍇ�i���w�E�F�b�W�j�A�������˂𒆐S�Ƃ������ɍL���p�x�ɂ킽��A�Ίp�͈��ƂȂ邩��ł���B���̂悤�ȃE�F�b�W�ɂ�����Ίp�͎��̎��ŋ�����B���in�\�P�j��